Two Tangents To A Circle

Line which touches a circle at exactly one point

In Euclidean plane geometry, a tangent line to a circumvolve is a line that touches the circle at exactly one betoken, never entering the circle's interior. Tangent lines to circles grade the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that bespeak, theorems involving tangent lines ofttimes involve radial lines and orthogonal circles.

Tangent lines to one circumvolve [edit]

A tangent line t to a circumvolve C intersects the circle at a single point T. For comparing, secant lines intersect a circumvolve at 2 points, whereas some other line may not intersect a circle at all. This property of tangent lines is preserved under many geometrical transformations, such equally scalings, rotation, translations, inversions, and map projections. In technical language, these transformations exercise not change the incidence structure of the tangent line and circle, even though the line and circle may be plain-featured.

The radius of a circle is perpendicular to the tangent line through its endpoint on the circle'southward circumference. Conversely, the perpendicular to a radius through the same endpoint is a tangent line. The resulting geometrical figure of circle and tangent line has a reflection symmetry about the axis of the radius.

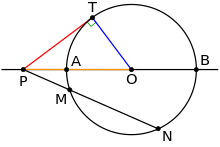
By the power-of-a-betoken theorem, the product of lengths PM·PN for any ray PMN equals to the square of PT, the length of the tangent line segment (red).

No tangent line can exist drawn through a signal inside a circle, since any such line must be a secant line. Nevertheless, ii tangent lines tin exist drawn to a circle from a indicate P outside of the circle. The geometrical figure of a circle and both tangent lines likewise has a reflection symmetry well-nigh the radial axis joining P to the eye point O of the circle. Thus the lengths of the segments from P to the 2 tangent points are equal. By the secant-tangent theorem, the square of this tangent length equals the power of the indicate P in the circle C. This power equals the product of distances from P to any two intersection points of the circle with a secant line passing through P.

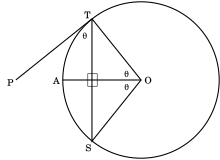
The angle θ between a chord and a tangent is half the arc belonging to the chord.

The tangent line t and the tangent indicate T have a conjugate relationship to one another, which has been generalized into the thought of pole points and polar lines. The aforementioned reciprocal relation exists between a indicate P exterior the circle and the secant line joining its two points of tangency.

If a bespeak P is exterior to a circle with center O, and if the tangent lines from P touch the circumvolve at points T and S, then ∠TPS and ∠TOS are supplementary (sum to 180°).

If a chord TM is drawn from the tangency point T of exterior betoken P and ∠PTM ≤ 90° then ∠PTM = (1/2)∠TOM.

Equation of the tangent line with coordinate [edit]

Suppose that the equation of the circumvolve is ${\displaystyle (x-a)^{ii}+(y-b)^{2}=r^{2}}$ with center at ${\displaystyle (a,b)}$ . Then the tangent line of the circle at ${\displaystyle (x_{1},y_{1})}$ is

${\displaystyle (x-x_{ane})(x_{1}-a)+(y-y_{1})(y_{1}-b)=0}$

This can be proved by taking the implicit derivative of the circle.

Compass and straightedge constructions [edit]

Information technology is relatively straightforward to construct a line t tangent to a circle at a bespeak T on the circumference of the circle:

• A line a is drawn from O, the center of the circle, through the radial point T;
• The line t is the perpendicular line to a.

Structure of a tangent to a given circle (black) from a given exterior bespeak (P).

Thales' theorem may be used to construct the tangent lines to a indicate P external to the circle C:

• A circle is drawn centered on the midpoint of the line segment OP, having diameter OP, where O is again the center of the circumvolve C.
• The intersection points T _one and T _two of the circle C and the new circle are the tangent points for lines passing through P, by the following argument.

The line segments OT₁ and OT_ii are radii of the circumvolve C; since both are inscribed in a semicircle, they are perpendicular to the line segments PT_i and PT_ii, respectively. Simply just a tangent line is perpendicular to the radial line. Hence, the two lines from P and passing through T _i and T ₂ are tangent to the circle C.

Another method to construct the tangent lines to a point P external to the circle using only a straightedge:

• Depict whatsoever three different lines through the given point P that intersect the circle twice.
• Let ${\displaystyle A_{1},A_{ii},B_{ane},B_{ii},C_{1},C_{ii}}$ exist the six intersection points, with the same letter of the alphabet respective to the same line and the index 1 respective to the signal closer to P.
• Allow D be the point where the lines ${\displaystyle A_{one}B_{2}}$ and ${\displaystyle A_{ii}B_{1}}$ intersect,
• Similarly E for the lines ${\displaystyle B_{1}C_{two}}$ and ${\displaystyle B_{ii}C_{1}}$ .
• Depict a line through D and Eastward.
• This line meets the circle at two points, F and K.
• The tangents are the lines PF and PG.^[1]

With analytic geometry [edit]

Let ${\displaystyle P=(a,b)}$ be a point of the circle with equation ${\displaystyle x^{two}+y^{2}=r^{ii}}$ . The tangent at ${\displaystyle P}$ has equation ${\displaystyle ax+by=r^{2}}$ , because ${\displaystyle P}$ lies on both the curves and ${\displaystyle {\vec {OP}}=(a,b)^{T}}$ is a normal vector of the line. The tangent intersects the x-centrality at bespeak ${\displaystyle P_{0}=(x_{0},0)}$ with ${\displaystyle ax_{0}=r^{ii}}$ .

Conversely, if one starts with point ${\displaystyle P_{0}=(x_{0},0)}$ , than the two tangents through ${\displaystyle P_{0}}$ encounter the circle at the 2 points ${\displaystyle P_{i/ii}=(a,b_{\pm })}$ with

${\displaystyle a={\frac {r^{two}}{x_{0}}},\qquad b_{\pm }=\pm {\sqrt {r^{2}-a^{2}}}=\pm {\frac {r}{x_{0}}}{\sqrt {x_{0}^{2}-r^{2}}}\quad }$ . Written in vector course:

${\displaystyle {\binom {a}{b_{\pm }}}={\frac {r^{2}}{x_{0}}}{\binom {1}{0}}\pm {\frac {r}{x_{0}}}{\sqrt {x_{0}^{2}-r^{two}}}{\binom {0}{1}}\ .}$

If bespeak ${\displaystyle P_{0}=(x_{0},y_{0})}$ lies not on the x-centrality: In the vector form 1 replaces ${\displaystyle x_{0}}$ by the distance ${\displaystyle \ d_{0}={\sqrt {x_{0}^{2}+y_{0}^{2}}}\ }$ and the unit of measurement base vectors past the orthogonal unit vectors ${\displaystyle \ {\vec {eastward}}_{1}={\frac {1}{d_{0}}}{\binom {x_{0}}{y_{0}}},\ {\vec {e}}_{2}={\frac {1}{d_{0}}}{\binom {-y_{0}}{x_{0}}}\ }$ . Then the tangents through betoken ${\displaystyle P_{0}}$ bear on the circle at the points

${\displaystyle {\binom {x_{1/two}}{y_{1/2}}}={\frac {r^{2}}{d_{0}^{2}}}{\binom {x_{0}}{y_{0}}}\pm {\frac {r}{d_{0}^{2}}}{\sqrt {d_{0}^{2}-r^{two}}}{\binom {-y_{0}}{x_{0}}}\ .}$

For ${\displaystyle d_{0}<r}$ no tangents exist.
For ${\displaystyle d_{0}=r}$ point ${\displaystyle P_{0}}$ lies on the circumvolve and there is just 1 tangent with equation ${\displaystyle x_{0}ten+y_{0}y=r^{2}}$ .
In case of ${\displaystyle d_{0}>r}$ there are 2 tangents with equations ${\displaystyle \ x_{one}10+y_{one}y=r^{two},\ x_{ii}x+y_{2}y=r^{ii}}$ .

Relation to circumvolve inversion: Equation ${\displaystyle ax_{0}=r^{2}}$ describes the circumvolve inversion of point ${\displaystyle (x_{0},0)}$ .

Relation to pole and polar: The polar of point ${\displaystyle (x_{0},0)}$ has equation ${\displaystyle xx_{0}=r^{2}}$ .

Tangential polygons [edit]

A tangential polygon is a polygon each of whose sides is tangent to a item circle, called its incircle. Every triangle is a tangential polygon, as is every regular polygon of whatsoever number of sides; in addition, for every number of polygon sides at that place are an infinite number of non-congruent tangential polygons.

Tangent quadrilateral theorem and inscribed circles [edit]

A tangential quadrilateral ABCD is a closed figure of four straight sides that are tangent to a given circle C. Equivalently, the circle C is inscribed in the quadrilateral ABCD. By the Pitot theorem, the sums of opposite sides of any such quadrilateral are equal, i.e.,

${\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}$

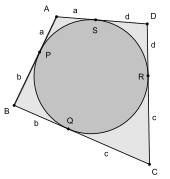
This conclusion follows from the equality of the tangent segments from the four vertices of the quadrilateral. Allow the tangent points be denoted as P (on segment AB), Q (on segment BC), R (on segment CD) and S (on segment DA). The symmetric tangent segments about each betoken of ABCD are equal, east.g., BP=BQ=b, CQ=CR=c, DR=DS=d, and AS=AP=a. Only each side of the quadrilateral is equanimous of ii such tangent segments

${\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)}$

proving the theorem.

The converse is also true: a circumvolve can be inscribed into every quadrilateral in which the lengths of opposite sides sum to the aforementioned value.^[2]

This theorem and its converse have various uses. For example, they show immediately that no rectangle tin can have an inscribed circle unless information technology is a square, and that every rhombus has an inscribed circle, whereas a general parallelogram does not.

Tangent lines to 2 circles [edit]

For two circles, there are generally four singled-out lines that are tangent to both (bitangent) – if the ii circles are outside each other – merely in degenerate cases there may exist any number betwixt zilch and 4 bitangent lines; these are addressed below. For 2 of these, the external tangent lines, the circles fall on the same side of the line; for the two others, the internal tangent lines, the circles fall on opposite sides of the line. The external tangent lines intersect in the external homothetic center, whereas the internal tangent lines intersect at the internal homothetic center. Both the external and internal homothetic centers lie on the line of centers (the line connecting the centers of the two circles), closer to the center of the smaller circle: the internal center is in the segment between the ii circles, while the external center is not between the points, but rather outside, on the side of the center of the smaller circle. If the two circles have equal radius, there are still four bitangents, but the external tangent lines are parallel and there is no external center in the affine plane; in the projective plane, the external homothetic center lies at the point at infinity corresponding to the gradient of these lines.^[three]

Outer tangent [edit]

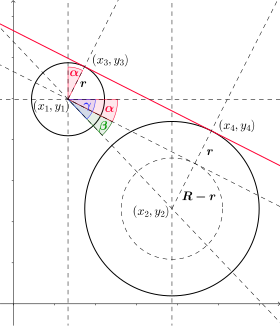
Finding outer tangent. Two circles' outer tangents.

The red line joining the points ${\displaystyle (x_{3},y_{3})}$ and ${\displaystyle (x_{4},y_{four})}$ is the outer tangent between the ii circles. Given points ${\displaystyle (x_{1},y_{ane})}$ , ${\displaystyle (x_{two},y_{ii})}$ the points ${\displaystyle (x_{three},y_{3})}$ , ${\displaystyle (x_{iv},y_{4})}$ can easily be calculated with help of the bending ${\displaystyle \blastoff }$ :

${\displaystyle {\brainstorm{aligned}x_{3}&=x_{one}\pm r\sin \blastoff \\y_{iii}&=y_{1}\pm r\cos \alpha \\x_{4}&=x_{ii}\pm R\sin \alpha \\y_{4}&=y_{2}\pm R\cos \alpha \\\end{aligned}}}$

Hither R and r notate the radii of the two circles and the angle ${\displaystyle \blastoff }$ can exist computed using bones trigonometry. You have ${\displaystyle \alpha =\gamma -\beta }$ with ${\displaystyle \gamma =-\arctan \left({\tfrac {y_{2}-y_{i}}{x_{2}-x_{i}}}\right)}$ and ${\displaystyle \beta =\pm \arcsin \left({\tfrac {R-r}{\sqrt {(x_{two}-x_{ane})^{2}+(y_{2}-y_{i})^{2}}}}\right)}$ . ^{[4] [ failed verification – come across discussion]}

Inner tangent [edit]

Inner tangent. The external tangent lines pass through the internal homothetic center.

An inner tangent is a tangent that intersects the segment joining two circles' centers. Note that the inner tangent will not be defined for cases when the two circles overlap.

Construction [edit]

The bitangent lines can be constructed either by amalgam the homothetic centers, as described at that article, and and so amalgam the tangent lines through the homothetic centre that is tangent to one circle, by one of the methods described above. The resulting line will and so be tangent to the other circle as well. Alternatively, the tangent lines and tangent points can be constructed more than directly, every bit detailed below. Notation that in degenerate cases these constructions break downwards; to simplify exposition this is not discussed in this section, but a class of the construction can work in limit cases (e.thousand., two circles tangent at one point).

Synthetic geometry [edit]

Let O ₁ and O _ii be the centers of the two circles, C _ane and C ₂ and let r _i and r ₂ exist their radii, with r _i >r ₂; in other words, circle C ₁ is defined as the larger of the two circles. Two unlike methods may be used to construct the external and internal tangent lines.

External tangents

Structure of the outer tangent

A new circle C ₃ of radius r ₁ −r ₂ is fatigued centered on O _i. Using the method above, 2 lines are fatigued from O ₂ that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking both circles C _ane and C ₂ by a constant corporeality, r ₂, which shrinks C _two to a betoken. Two radial lines may exist fatigued from the eye O ₁ through the tangent points on C ₃; these intersect C ₁ at the desired tangent points. The desired external tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be synthetic every bit described higher up.

Internal tangents

Construction of the inner tangent

A new circle C _three of radius r _i +r ₂ is drawn centered on O ₁. Using the method above, two lines are drawn from O ₂ that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking C ₂ to a point while expanding C ₁ by a constant amount, r ₂. Two radial lines may be fatigued from the center O ₁ through the tangent points on C ₃; these intersect C ₁ at the desired tangent points. The desired internal tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be constructed as described higher up.

Analytic geometry [edit]

Permit the circles have centres c ₁ = (x _one,y ₁) and c _two = (x ₂,y _two) with radius r _i and r ₂ respectively. Expressing a line by the equation ${\displaystyle ax+by+c=0,}$ with the normalization a ² +b ^two = 1, then a bitangent line satisfies:

ax ₁ +past ₁ +c =r ₁ and

ax _two +by _two +c =r ₂.

Solving for ${\displaystyle (a,b,c)}$ by subtracting the first from the second yields

aΔten +bΔy = Δr

where Δx =x ₂ −x _i, Δy =y _ii −y ₁ and Δr =r ₂ −r ₁.

If ${\displaystyle d={\sqrt {(\Delta x)^{ii}+(\Delta y)^{2}}}}$ is the distance from c ₁ to c ₂ we can normalize by Ten = Δx/d, Y = Δy/d and R = Δr/d to simplify equations, yielding the equations aX +bY =R and a ⁱⁱ +b ² = i, solve these to go ii solutions (k = ±1) for the 2 external tangent lines:

a =RX −kY√(1 −R ²)

b =RY +kX√(1 −R ²)

c =r ₁ − (ax _one +by _i)

Geometrically this corresponds to computing the bending formed by the tangent lines and the line of centers, so using that to rotate the equation for the line of centers to yield an equation for the tangent line. The angle is computed by calculating the trigonometric functions of a right triangle whose vertices are the (external) homothetic center, a center of a circumvolve, and a tangent point; the hypotenuse lies on the tangent line, the radius is contrary the bending, and the adjacent side lies on the line of centers.

(X,Y) is the unit vector pointing from c _ane to c ₂, while R is ${\displaystyle \cos \theta }$ where ${\displaystyle \theta }$ is the angle between the line of centers and a tangent line. ${\displaystyle \sin \theta }$ is then ${\displaystyle \pm {\sqrt {ane-R^{2}}}}$ (depending on the sign of ${\displaystyle \theta }$ , equivalently the direction of rotation), and the above equations are rotation of (10,Y) by ${\displaystyle \pm \theta ,}$ using the rotation matrix:

${\displaystyle {\begin{pmatrix}R&\mp {\sqrt {1-R^{2}}}\\\pm {\sqrt {1-R^{two}}}&R\end{pmatrix}}}$

k = 1 is the tangent line to the right of the circles looking from c ₁ to c ₂.

k = −one is the tangent line to the right of the circles looking from c ₂ to c ₁.

The above assumes each circumvolve has positive radius. If r _ane is positive and r _two negative then c ₁ volition lie to the left of each line and c ₂ to the right, and the two tangent lines volition cross. In this manner all four solutions are obtained. Switching signs of both radii switches 1000 = 1 and 1000 = −1.

Vectors [edit]

Finding outer tangent. Circle tangents.

In full general the points of tangency t _i and t _two for the four lines tangent to 2 circles with centers v _one and v ₂ and radii r ₁ and r _two are given by solving the simultaneous equations:

${\displaystyle {\begin{aligned}(t_{two}-v_{two})\cdot (t_{2}-t_{1})&=0\\(t_{1}-v_{one})\cdot (t_{ii}-t_{1})&=0\\(t_{1}-v_{1})\cdot (t_{i}-v_{i})&=r_{i}^{two}\\(t_{2}-v_{two})\cdot (t_{ii}-v_{2})&=r_{ii}^{two}\\\end{aligned}}}$

These equations express that the tangent line, which is parallel to ${\displaystyle t_{2}-t_{ane},}$ is perpendicular to the radii, and that the tangent points lie on their respective circles.

These are four quadratic equations in two two-dimensional vector variables, and in general position will have 4 pairs of solutions.

Degenerate cases [edit]

Two singled-out circles may take between zero and four bitangent lines, depending on configuration; these can be classified in terms of the distance between the centers and the radii. If counted with multiplicity (counting a mutual tangent twice) there are zero, two, or 4 bitangent lines. Bitangent lines can also be generalized to circles with negative or zero radius. The degenerate cases and the multiplicities can also be understood in terms of limits of other configurations – eastward.g., a limit of two circles that almost touch, and moving one and then that they touch, or a circle with small radius shrinking to a circle of cipher radius.

• If the circles are exterior each other ( ${\displaystyle d>r_{1}+r_{2}}$ ), which is general position, at that place are iv bitangents.
• If they touch externally at i signal ( ${\displaystyle d=r_{1}+r_{2}}$ ) – take one point of external tangency – then they take two external bitangents and one internal bitangent, namely the mutual tangent line. This common tangent line has multiplicity ii, every bit it separates the circles (ane on the left, one on the right) for either orientation (management).
• If the circles intersect in two points ( ${\displaystyle |r_{ane}-r_{2}|<d<r_{i}+r_{two}}$ ), and then they take no internal bitangents and ii external bitangents (they cannot be separated, considering they intersect, hence no internal bitangents).
• If the circles impact internally at ane indicate ( ${\displaystyle d=|r_{1}-r_{2}|}$ ) – have one point of internal tangency – then they take no internal bitangents and 1 external bitangent, namely the common tangent line, which has multiplicity two, as above.
• If one circumvolve is completely inside the other ( ${\displaystyle d<|r_{one}-r_{2}|}$ ) then they have no bitangents, as a tangent line to the outer circle does not intersect the inner circle, or conversely a tangent line to the inner circle is a secant line to the outer circumvolve.

Finally, if the ii circles are identical, any tangent to the circle is a common tangent and hence (external) bitangent, so there is a circumvolve'southward worth of bitangents.

Farther, the notion of bitangent lines tin exist extended to circles with negative radius (the same locus of points, ${\displaystyle x^{2}+y^{2}=(-r)^{two},}$ but considered "within out"), in which case if the radii accept opposite sign (one circle has negative radius and the other has positive radius) the external and internal homothetic centers and external and internal bitangents are switched, while if the radii have the aforementioned sign (both positive radii or both negative radii) "external" and "internal" have the same usual sense (switching one sign switches them, so switching both switches them dorsum).

Bitangent lines can also exist defined when one or both of the circles has radius zero. In this instance the circle with radius goose egg is a double point, and thus whatever line passing through it intersects the point with multiplicity two, hence is "tangent". If one circumvolve has radius nix, a bitangent line is simply a line tangent to the circle and passing through the point, and is counted with multiplicity 2. If both circles accept radius zero, then the bitangent line is the line they define, and is counted with multiplicity four.

Note that in these degenerate cases the external and internal homothetic center do generally still be (the external center is at infinity if the radii are equal), except if the circles coincide, in which case the external center is not defined, or if both circles accept radius zero, in which case the internal center is not defined.

Applications [edit]

Belt problem [edit]

The internal and external tangent lines are useful in solving the belt problem, which is to calculate the length of a belt or rope needed to fit snugly over two pulleys. If the belt is considered to be a mathematical line of negligible thickness, and if both pulleys are causeless to lie in exactly the same aeroplane, the trouble devolves to summing the lengths of the relevant tangent line segments with the lengths of round arcs subtended by the belt. If the belt is wrapped well-nigh the wheels so as to cantankerous, the interior tangent line segments are relevant. Conversely, if the belt is wrapped exteriorly effectually the pulleys, the exterior tangent line segments are relevant; this example is sometimes called the pulley problem.

Tangent lines to three circles: Monge's theorem [edit]

For iii circles denoted by C ₁, C _two, and C _iii, there are iii pairs of circles (C _one C _two, C ₂ C ₃, and C ₁ C ₃). Since each pair of circles has two homothetic centers, in that location are six homothetic centers birthday. Gaspard Monge showed in the early on 19th century that these six points prevarication on iv lines, each line having three collinear points.

Trouble of Apollonius [edit]

Animation showing the inversive transformation of an Apollonius trouble. The blue and ruby circles dandy to tangency, and are inverted in the grayness circle, producing two directly lines. The yellow solutions are institute past sliding a circle between them until information technology touches the transformed green circle from within or without.

Many special cases of Apollonius's problem involve finding a circle that is tangent to one or more than lines. The simplest of these is to construct circles that are tangent to three given lines (the LLL problem). To solve this problem, the eye of any such circumvolve must prevarication on an angle bisector of any pair of the lines; there are two angle-bisecting lines for every intersection of two lines. The intersections of these angle bisectors give the centers of solution circles. In that location are 4 such circles in general, the inscribed circumvolve of the triangle formed past the intersection of the three lines, and the 3 exscribed circles.

A general Apollonius problem tin can be transformed into the simpler problem of circle tangent to one circumvolve and two parallel lines (itself a special case of the LLC special case). To accomplish this, it suffices to scale ii of the three given circles until they merely touch, i.e., are tangent. An inversion in their tangent signal with respect to a circumvolve of appropriate radius transforms the two touching given circles into two parallel lines, and the third given circle into another circle. Thus, the solutions may be constitute by sliding a circumvolve of abiding radius between two parallel lines until information technology contacts the transformed tertiary circle. Re-inversion produces the respective solutions to the original problem.

Generalizations [edit]

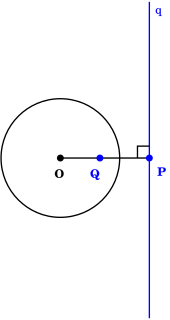
The concept of a tangent line and tangent point tin exist generalized to a pole bespeak Q and its respective polar line q. The points P and Q are inverses of each other with respect to the circle.

The concept of a tangent line to 1 or more circles can be generalized in several ways. Outset, the conjugate relationship between tangent points and tangent lines tin can be generalized to pole points and polar lines, in which the pole points may be anywhere, non only on the circumference of the circle. 2nd, the wedlock of two circles is a special (reducible) example of a quartic plane curve, and the external and internal tangent lines are the bitangents to this quartic curve. A generic quartic bend has 28 bitangents.

A third generalization considers tangent circles, rather than tangent lines; a tangent line can be considered as a tangent circle of infinite radius. In item, the external tangent lines to 2 circles are limiting cases of a family of circles which are internally or externally tangent to both circles, while the internal tangent lines are limiting cases of a family unit of circles which are internally tangent to ane and externally tangent to the other of the two circles.^[five]

In Möbius or inversive geometry, lines are viewed equally circles through a indicate "at infinity" and for any line and any circle, there is a Möbius transformation which maps one to the other. In Möbius geometry, tangency between a line and a circle becomes a special instance of tangency between two circles. This equivalence is extended farther in Lie sphere geometry.

Radius and tangent line are perpendicular at a point of a circumvolve, and hyperbolic-orthogonal at a point of the unit of measurement hyperbola. The parametric representation of the unit of measurement hyperbola via radius vector is ${\displaystyle p(a)\ =\ (\cosh a,\sinh a).}$ The derivative of p(a) points in the management of tangent line at p(a), and is ${\displaystyle {\frac {dp}{da}}\ =\ (\sinh a,\cosh a).}$ The radius and tangent are hyperbolic orthogonal at a since ${\displaystyle p(a)\ {\text{and}}\ {\frac {dp}{da}}}$ are reflections of each other in the asymptote y=10 of the unit of measurement hyperbola. When interpreted as dissever-complex numbers (where j j = +one), the ii numbers satisfy ${\displaystyle jp(a)\ =\ {\frac {dp}{da}}.}$

References [edit]

1. ^ "Finding tangents to a circle with a straightedge". Stack Exchange. August 15, 2015.
2. ^ Alexander Bogomolny "When A Quadrilateral Is Inscriptible?" at Cutting-the-knot
3. ^ Paul Kunkel. "Tangent circles". Whistleralley.com. Retrieved 2008-09-29 .
4. ^ Libeskind, Shlomo (2007), Euclidean and Transformational Geometry: A Deductive Inquiry, pp. 110–112 (online copy, p. 110, at Google Books)
5. ^ Kunkel, Paul (2007), "The tangency problem of Apollonius: three looks" (PDF), BSHM Bulletin: Journal of the British Society for the History of Mathematics, 22 (1): 34–46, doi:10.1080/17498430601148911, S2CID 122408307

External links [edit]

• Weisstein, Eric West. "Tangent lines to one circumvolve". MathWorld.
• Weisstein, Eric W. "Tangent lines to two circles". MathWorld.

Two Tangents To A Circle,

Source: https://en.wikipedia.org/wiki/Tangent_lines_to_circles

Posted by: daleybeirch.blogspot.com

Share this post