0 To The Third Power

Exponents Computer or eastward calculator is used in solving exponential forms of expressions. It is also known as raised to the power computer.

Backdrop of exponents computer:

This calculator solves bases with both negative exponents and positive exponents. It also provides a step by footstep method with an accurate respond.

What is an exponent?

An exponent is a small number located in the upper, right-mitt position of an exponential expression (base exponent), which indicates the power to which the base of the expression is raised.

The exponent of a number shows you how many times the number is to be used in a multiplication. Exponents do not have to be numbers or constants; they can be variables.

They are often positive whole numbers, just they tin can be negative numbers, fractional numbers, irrational numbers, or complex numbers. It is written as a small number to the right and above the base number.

Types:

There are basically 2 types of exponents.

Positive exponent

A positive exponent tells how many times a number is needed to be multiplied by itself. Apply our exponent estimator to solve your questions.

Negative exponent

A negative exponent represents which fraction of the base of operations, the solution is. To simplify exponents with power in the form of fractions, utilise our exponent figurer.

Instance:

Calculate the exponent for the 3 raised to the power of 4 (3 to the power of four).

It ways = iii⁴

Solution:

iii*3*3*iii = 81

4 to the third power = 81

Therefore the exponent is 81

2 raised to the ability figurer.

Case:

What is the value of exponent for ii enhance to ability 9 (ii to the 9th power)

It means = two^ix

Solution:

ii*2*ii*2*2*ii*2*two*ii = 512

2 to the ninth power = 512

Therefore the exponent is 512.

Example :

How practice you lot calculate the exponents of 5,six,seven to the ability of four?

Information technology means = 5⁴, vi⁴, 7⁴

Solution:

5*5*five*five = 625

6*6*6*six = 1296

seven*7*vii*seven = 2401

Therefore the exponents are 625, 1296, 2401.

How to calculate the nth ability of a number?

The nth ability of a base, allow's say "y", means y multiplied to itself nth time. If we are to find the fifth ability of y, it is y*y*y*y*y.

Some other solutions for the nth power calculator are in the following table.

0.1 to the power of three	0.00100
0.5 to the power of iii	0.12500
0.5 to the power of four	0.06250
1.2 to the power of 4	2.07360
ane.02 to the tenth power	1.21899
1.03 to the 10th power	1.34392
one.2 to the power of 5	2.48832
1.4 to the 10th power	28.92547
1.05 to the ability of 5	one.27628
ane.05 to the 10th ability	1.62889
one.06 to the tenth ability	ane.79085
2 to the third power	8
2 to the power of iii	8
two raised to the power of 4	16
2 to the power of half-dozen	64
2 to the power of 7	128
2 to the 9th power	512
2 to the tenth power	1024
2 to the 15th ability	32768
2 to the 10th power	1024
2 to the ability of 28	268435456
iii to the ability of 2	ix
3 to the 3 power	27
three to the 4 power	81
3 to the eighth ability	6561
three to the 9th power	19683
three to the twelfth power	531441
3 to what power equals 81	3^four
four to the power of 3	64
4 to the power of 4	256
iv to the power of 7	16384
7 to the power of 3	343
12 to the 2nd power	144
2.five to the power of iii	15.625
12 to the power of 3	1728
10 exponent 3	thou
24 to the 2nd ability (24²)	576
10 to the ability of 3	grand
3 to the power of five	243
half-dozen to the power of iii	216
9 to the power of 3	729
9 to the power of 2	81
10 to the power of five	100000

Exponent Rules:

Learning the exponent rules along with log rules can brand maths really piece of cake for understanding. In that location are 7 exponent rules.

Nothing Property of exponent:

It ways if the ability of a base is zip then the value of the solution will be i.

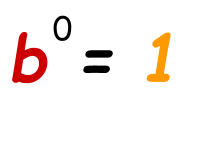
Case: Simplify five⁰.

In this question, the power of base is zero, then according to the zero holding of exponents, the reply of this not zero base of operations is 1. Hence,

5⁰= one

Negative Holding of exponent:

It means when the power of base is a negative number, then after multiplying nosotros will have to find the reciprocal of the reply.

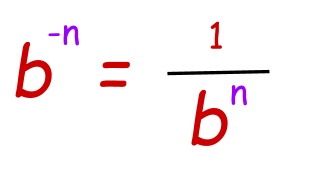
Case: Simplify ane/three^-2.

We volition offset make the ability positive by taking reciprocal.

1/3^-2=3²

three² = 9

Production Holding of exponent:

When two exponential expressions having the same non zero base and different powers are multiplied, then their powers are added over the aforementioned base.

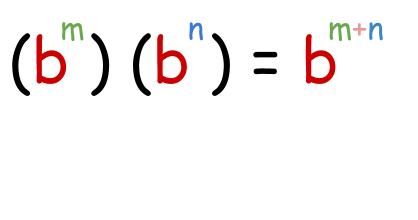
Example: Solve (two⁶)(2²).

Equally it is obvious, bases are the same so powers are to exist added. Now

(2⁶)(two²) = 2⁶⁺²

ii⁸ =2*two*two*2*2*ii*2*2

=256

Quotient Property of exponent:

It is the opposite of the product belongings of exponent. When two same bases having different exponents are required to be divided, so their powers are subtracted.

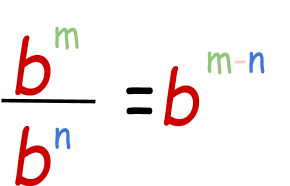
Example: Simplify 3⁷/3ⁱⁱ

iii⁷/ 3²=3^7-2

35=3*3*3*iii*3

= 243

Power of a Power Property:

When an exponent expression further has power, and so firstly y'all demand to multiply the powers and so solve the expression.

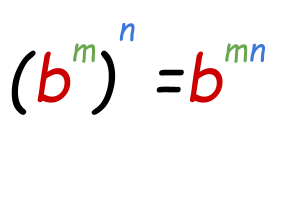
Example: Solve: ( ten²)³.

Keeping in view the power of power property of exponents, nosotros volition multiply powers.

(xⁱⁱ)³=x^ii*3

= x⁶

Ability of a product property:

When a product of bases is raised to some power, the bases will possess the power separately.

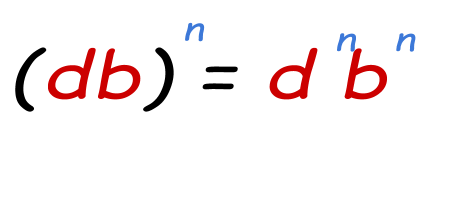
Example: Simplify (4*5)²

four ² * 5 ² =sixteen* 25

= 400

Power of a Quotient Property:

It is the same equally the power of a product property. Power belongs separately to both the numerator and denominator.

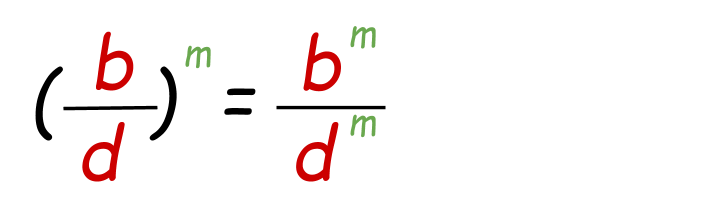
Example: Solve (2/3)²

(2/3)²=2^two/ 3²

two²/ 3²=4/nine